Set similarity measure finds its application spanning the Computer Science spectrum; some applications being - user segmentation, finding near-duplicate webpages/documents, clustering, recommendation generation, sequence alignment, and many more. In this essay, we take a detailed look into a set-similarity measure called - Jaccard’s Similarity Coefficient and how its computation can be optimized using a neat technique called MinHash.
Jaccard Similarity Coefficient
Jaccard Similarity Coefficient quantifies how similar two finite sets really are and is defined as the size of their intersection divided by the size of their union. This similarity measure is very intuitive and we can clearly see that it is a real-valued measure bounded in the interval [0, 1].

The coefficient is 0 when the two sets are mutually exclusive (disjoint) and it is 1 when the sets are equal. Below we see the one-line python function that computes this similarity measure.
def similarity_jaccard(a: set, b: set) -> float:
return len(a.intersection(b)) / len(a.union(b))Jaccard Similarity Coefficient as Probability
Jaccard Coefficient can also be interpreted as the probability that an element picked at random from the universal set U is present in both sets A and B.

Another analogy for this probability is the chances of throwing a dart and it hitting the intersection. Thus we see how we can transform the Jaccard Similarity Coefficient into a simple probability statement. This will come in very handy when we try to optimize the computation at scale.
Problem at Scale
Computing Jaccard Similarity Coefficient is very simple, all we require is a union operation and an intersection operation on the participating sets. But these computations go haywire when things run at scale.
Computing set similarity is usually a subproblem fitting in a bigger picture, for example, near-duplicate detection which finds near-duplicate articles across millions of documents. When we tokenize the documents and apply raw Jaccard Similarity Coefficient for every two combinations of documents we find that the computation will take years.
Instead of finding the true value for this coefficient, we can rely on an approximation if we can get a considerable speedup and this is where a technique called MinHash fits well.
MinHash
MinHash algorithm gives us a fast approximation to the Jaccard Similarity Coefficient between any two finite sets. Instead of computing the unions and the intersections every single time, this method once creates MinHash Signature for each set and use it to approximate the coefficient.
Computing single MinHash
MinHash h of the set S is the index of the first element, from a permuted Universal Set, that is present in the set S. But since permutation is a computation heavy operation especially for large sets we use a hashing/mapping function that typically reorders the elements using simple math operation. One such hashing function is

If u is the total number of elements in the Universal Set U then a and b are the random integers less than u and c is the prime number slightly higher than u. A sample permute function could be
def permute_fn(x: int) -> int:
return (23 * x + 67) % 199Now that we have defined permutation as a simple mathematical operation that spits out the new row index, we can find MinHash of a set as the element that has the minimum new row number. Hence we can define the MinHash function as
def minhash(s: set) -> int:
return min([permute_fn(e) for e in s])A surprising property of MinHash
MinHash has a surprising property, according to which, the probability that the MinHash of random permutation produces the same value for the two sets equals the Jaccard Similarity Coefficient of those sets.
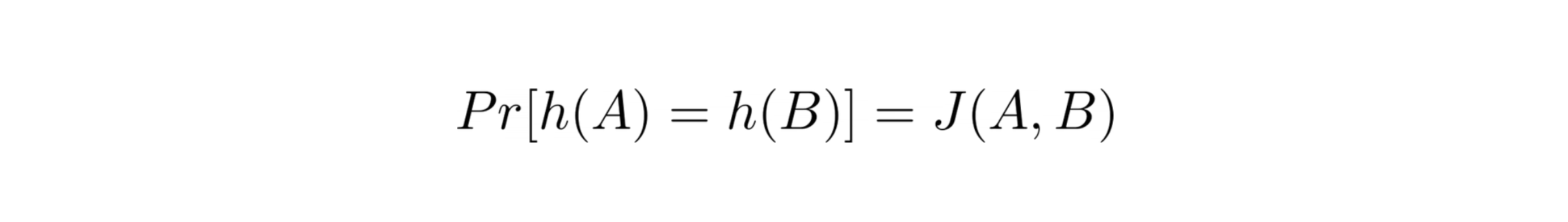
The above equality holds true because the probability of MinHash of two sets to be the same is the number of elements present in both the sets divided by the total number of elements in both the sets combined; which in fact is the definition of Jaccard Similarity Coefficient.
Hence to approximate Similarity Coefficient using MinHash all we have to do is find the Probability of MinHash of two sets to be the same, and this is where the MinHash Signature comes in to play.
MinHash Signature
MinHash Signature of a set S is a collection of k MinHash values corresponding to k different MinHash functions. The size k depends on the error tolerance, keeping it higher leads to more accurate approximations.
def minhash_signature(s: set):
return [minhash(s) for minhash in minhash_fns]MinHash functions usually differ in the permutation parameters i.e. coefficients
a,bandc.
Now in order to compute Pr[h(A) = h(B)] we have to compare the MinHash Signature of the participating sets A and B and find how many values in their signatures match; dividing this number by the number of hash functions k will give the required probability and in turn an approximation of Jaccard Similarity Coefficient.
def similarity_minhash(a: set, b: set) -> float:
sign_a = minhash_signature(a)
sign_b = minhash_signature(b)
return sum([1 for a, b in zip(sign_a, sign_b) if a == b]) / len(sign_a)MinHash Signature could well be computed just once per set.
Thus to compute set similarity, we need not perform heavy computation like Union and Intersection and that too across millions of sets at scale, rather we can simply compare k items of in their signatures and get a fairly good estimate of it.
How good is the estimate?
In order to find how close the estimate is we compute the Jaccard Similarity Coefficient and its approximate using MinHash on two disjoint sets having equal cardinality. One of the sets will undergo a transition where one element of it will be replaced with one element of the other set. So with time, the sets will go from disjoint to being equal.

The illustration above shows the two plots and we can clearly see that the MinHash technique provides a fairly good estimate of Jaccard Similarity Coefficient with much fewer computations.
